| Name | Econ_Domain | Social_Domain | Env_Domain | |
|---|---|---|---|---|
| 0 | Aberdeen, SD Micro Area | 0.565264 | 0.591259 | 0.444472 |
| 1 | Aberdeen, WA Micro Area | 0.427671 | 0.520744 | 0.429274 |
Density estimation, mixture models, and smoothing
Invalid Date
Outline for today
- More on density estimation
- non-Gaussian kernels
- multivariate KDE
- mixture models
- Scatterplot smoothing
- Kernel smoothing
- LOESS
Sustainability data
We’ll work with sustainability index data for US cities to explore density estimation further.
- 933 distinct cities
- indices for sustainability in enviornmental, social, and eonomic domains
Environmental sustainability index
Let’s use the environmental sustainability index (Env_Domain) initially. The distribution of environmental sustainability across cities is shown below.
Code
hist = alt.Chart(
sust
).transform_bin(
'esi',
field = 'Env_Domain',
bin = alt.Bin(step = 0.02)
).transform_aggregate(
count = 'count()',
groupby = ['esi']
).transform_calculate(
Density = 'datum.count/(0.02*933)',
ESI = 'datum.esi + 0.01'
).mark_bar(size = 8).encode(
x = 'ESI:Q',
y = 'Density:Q'
)
hist.configure_axis(
labelFontSize = 14,
titleFontSize = 16
)KDE bandwidth selection
A common choice for Gaussian KDE bandwidth is Scott’s rule:
b=1.06×s×n−1/5
Code
# bandwitdth parameter
n, p = sust.shape
sigma_hat = sust.Env_Domain.std()
bw_scott = 1.06*sigma_hat*n**(-1/5)
# plot
smooth = alt.Chart(
sust
).transform_density(
'Env_Domain',
as_ = ['Environmental sustainability index', 'Density'],
extent = [0.1, 0.8],
bandwidth = bw_scott
).mark_line(color = 'black').encode(
x = 'Environmental sustainability index:Q',
y = 'Density:Q'
)
(hist + smooth).configure_axis(
labelFontSize = 14,
titleFontSize = 16
)KDEs with statsmodels
The statsmodels package has KDE implementations with finer control. This will allow us to experiment with other kernels.
Other kernels
Now let’s try varying the kernel. The ‘local histogram’ introduced last lecture is a KDE with a uniform kernel.
Code
# compute density estimate
kde = sm.nonparametric.KDEUnivariate(sust.Env_Domain)
kde.fit(kernel = 'uni', fft = False, bw = 0.02)
# arrange as dataframe
kde_df = pd.DataFrame({'Environmental sustainability index': kde.support, 'Density': kde.density})
# plot
smooth2 = alt.Chart(
kde_df
).mark_line(color = 'black').encode(
x = 'Environmental sustainability index:Q',
y = alt.Y('Density:Q', scale = alt.Scale(domain = [0, 12]))
)
(hist + smooth2 + smooth2.mark_area(opacity = 0.3)).configure_axis(
labelFontSize = 14,
titleFontSize = 16
)Other kernels
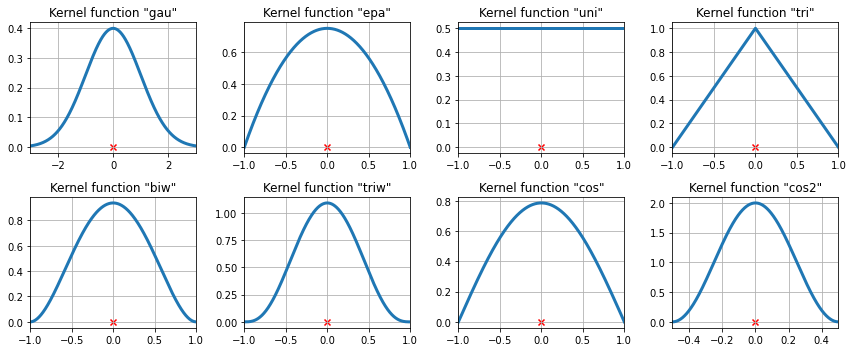
- Titles indicate
statsmodels.nonparametric.KDEUnivariateabbreviations - Note different axis scales – not as similar as they look!
Explore
Take 5-6 minutes with your neighbor and use the activity notebook to experiment and answer the following.
- How does the KDE differ if a parabolic (
epa) kernel is used in place of a Gaussian (gau) kernel while the bandwidth is held constant? - What effect does a triangular kernel (
tri) have on how local peaks appear? - Pick two kernels. What will happen to the KDE for large bandwidths?
- Which kernel seems to do the best job at capturing the shape closely without under-smoothing?
Multivariate KDE
Now let’s estimate the joint distribution of environmental and economic sustainability indices. Here are the values:
Multivariate histograms
There are a few options for displaying a 2-D histogram. One is to bin and plot a heatmap, as we saw before:
Code
alt.Chart(
sust
).mark_rect().encode(
x = alt.X('Env_Domain', bin = alt.Bin(maxbins = 40), title = 'Environmental sustainability'),
y = alt.Y('Econ_Domain', bin = alt.Bin(maxbins = 40), title = 'Economic sustainability'),
color = alt.Color('count()', scale = alt.Scale(scheme = 'bluepurple'), title = 'Number of U.S. cities')
).configure_axis(
labelFontSize = 14,
titleFontSize = 16
).configure_legend(
labelFontSize = 14,
titleFontSize = 16
)Multivariate histograms
Another option is to make a bubble chart with the size of the bubble proportional to the count of observations in the corresponding bin:
Code
alt.Chart(
sust
).mark_circle().encode(
x = alt.X('Env_Domain', bin = alt.Bin(maxbins = 40), title = 'Environmental sustainability'),
y = alt.Y('Econ_Domain', bin = alt.Bin(maxbins = 40), title = 'Economic sustainability'),
size = alt.Size('count()', scale = alt.Scale(scheme = 'bluepurple'))
).configure_axis(
labelFontSize = 14,
titleFontSize = 16
).configure_legend(
labelFontSize = 14,
titleFontSize = 16
)Multivariate KDE
The following computes a multivariate Gaussian KDE
# retrieve data as 2-d array (num observations, num variables)
fit_ary = sust.loc[:, ['Env_Domain', 'Econ_Domain']].values
# compute KDE
kde = sm.nonparametric.KDEMultivariate(data = fit_ary, var_type = 'cc')
kdeKDE instance
Number of variables: k_vars = 2
Number of samples: nobs = 933
Variable types: cc
BW selection method: normal_reference- input: 2-D array (observations×variables)
- variable type specification, one per variate: continuous, discrete, etc.
- method of bandwidth selection (not shown)
Prediction grids
A common visualization strategy is to generate a prediction grid: a mesh of values spanning a domain of interest, for the purpose of computing a function at each grid point.
Here is a 20 x 20 mesh:
Code
# resolution of grid (number of points to use along each axis)
grid_res = 20
# find grid point coordinates along each axis
x1 = np.linspace(start = sust.Env_Domain.min(), stop = sust.Env_Domain.max(), num = grid_res)
x2 = np.linspace(start = sust.Econ_Domain.min(), stop = sust.Econ_Domain.max(), num = grid_res)
# generate a mesh from the coordinates
grid1, grid2 = np.meshgrid(x1, x2, indexing = 'ij')
grid_ary = np.array([grid1.ravel(), grid2.ravel()]).T
# plot grid points
alt.Chart(
pd.DataFrame(grid_ary).rename(columns = {0: 'env', 1: 'econ'})
).mark_point(color = 'black').encode(
x = alt.X('env', scale = alt.Scale(zero = False)),
y = alt.Y('econ', scale = alt.Scale(zero = False))
).configure_axis(
labelFontSize = 14,
titleFontSize = 16
)Prediction grids
We’ll use a 100 x 100 mesh and kde.pdf() to compute the estimated density at each grid point:
Code
# resolution of grid (number of points to use along each axis)
grid_res = 100
# find grid point coordinates along each axis
x1 = np.linspace(start = sust.Env_Domain.min(), stop = sust.Env_Domain.max(), num = grid_res)
x2 = np.linspace(start = sust.Econ_Domain.min(), stop = sust.Econ_Domain.max(), num = grid_res)
# generate a mesh from the coordinates
grid1, grid2 = np.meshgrid(x1, x2, indexing = 'ij')
grid_ary = np.array([grid1.ravel(), grid2.ravel()]).T
# compute the density at each grid point
f_hat = kde.pdf(grid_ary)
# rearrange as a dataframe
grid_df = pd.DataFrame({'env': grid1.reshape(grid_res**2),
'econ': grid2.reshape(grid_res**2),
'density': f_hat})
# preview, for understanding
grid_df.head()| env | econ | density | |
|---|---|---|---|
| 0 | 0.132467 | 0.143811 | 1.325548e-17 |
| 1 | 0.132467 | 0.150278 | 6.367762e-17 |
| 2 | 0.132467 | 0.156745 | 2.929104e-16 |
| 3 | 0.132467 | 0.163212 | 1.290785e-15 |
| 4 | 0.132467 | 0.169679 | 5.451826e-15 |
Multivariate KDE heatmap
Code
# kde
kde_smooth = alt.Chart(
grid_df, title = 'Gaussian KDE'
).mark_rect(opacity = 0.8).encode(
x = alt.X('env', bin = alt.Bin(maxbins = grid_res), title = 'Environmental sustainability'),
y = alt.Y('econ', bin = alt.Bin(maxbins = grid_res), title = 'Economic sustainability'),
color = alt.Color('mean(density)', # a bit hacky, but works
scale = alt.Scale(scheme = 'bluepurple', type = 'sqrt'),
title = 'Density')
)
# histogram
bubble = alt.Chart(
sust
).mark_circle().encode(
x = alt.X('Env_Domain', bin = alt.Bin(maxbins = 40), title = 'Environmental sustainability'),
y = alt.Y('Econ_Domain', bin = alt.Bin(maxbins = 40), title = 'Economic sustainability'),
size = alt.Size('count()', scale = alt.Scale(scheme = 'bluepurple'), title = 'Cities')
)
# layer
(bubble + kde_smooth).configure_axis(
labelFontSize = 14,
titleFontSize = 16
).configure_legend(
labelFontSize = 14,
titleFontSize = 16
)- Does the KDE seem like a good estimate?
- What, if anything, does the graphic convey about the sustainability of cities?
Mixture models
KDE is a nonparametric technique: it involves no population parameters.
Mixture models are a parametric alternative for density estimation. The Gaussian mixture model is: f(x)=a1φ(x;μ1,σ1)+⋯+anφ(x;μn,σn)
- f(x) is the distribution of interest
- φ(⋅;μ,σ) denotes a Gaussian density with mean μ and standard deviation σ
- the model has n components
- a1,…,an are the mixing parameters
- fitted using the EM algorithm
Bivariate mixture model
Let’s fit a mixture to the joint distribution of environmental and economic sustainability indices:
We can inspect the estimated components’ centers (means):
Bivariate mixture model
Code
# evaluate log-likelihood
grid_df['gmm'] = np.exp(gmm.score_samples(grid_ary))
# gmm
gmm_smooth = alt.Chart(
grid_df, title = 'GMM'
).mark_rect(opacity = 0.8).encode(
x = alt.X('env', bin = alt.Bin(maxbins = grid_res), title = 'Environmental sustainability'),
y = alt.Y('econ', bin = alt.Bin(maxbins = grid_res), title = 'Economic sustainability'),
color = alt.Color('mean(gmm)', # a bit hacky, but works
scale = alt.Scale(scheme = 'bluepurple', type = 'sqrt'),
title = 'Density')
)
# centers of mixture components
ctr = alt.Chart(centers).mark_point(color = 'black', shape = 'triangle').encode(x = 'env', y = 'econ')
((bubble + gmm_smooth + ctr) | (bubble + kde_smooth)).configure_axis(
labelFontSize = 14,
titleFontSize = 16
).configure_legend(
labelFontSize = 14,
titleFontSize = 16
)- What differences do you observe?
- Which do you prefer and why?
Pros and Cons
KDE is a nonparametric method and is sometimes called a memory-based procedure: it uses all available data every time an estimated value is calculated.
- Advantages: minimal assumptions, highly flexible
- Disadvantages: not parsimonious, computationally intensive
GMM’s are parametric models.
- Advantages: closed-form structure, good for multimodal distributions, various kinds of inference and prediction are possible
- Disadvantages: estimation is less straightforward, may over-smooth, possible identifiability issues
GMMs for capturing subpopulations
The GMM is especially useful if there are latent subpopulations in the data. Recall the simulated population of hawks:
Code
# for reproducibility
np.random.seed(40721)
# simulate hypothetical population
female_hawks = pd.DataFrame(
data = {'length': np.random.normal(loc = 57.5, scale = 3, size = 3000),
'sex': np.repeat('female', 3000)}
)
male_hawks = pd.DataFrame(
data = {'length': np.random.normal(loc = 50.5, scale = 3, size = 2000),
'sex': np.repeat('male', 2000)}
)
population_hawks = pd.concat([female_hawks, male_hawks], axis = 0)
population_hawks.groupby('sex').head(1)| length | sex | |
|---|---|---|
| 0 | 53.975230 | female |
| 0 | 53.076663 | male |
Hawks
The histogram is not obviously bimodal, but we can suppose we’re aware of the sex differences in length and just don’t have that information.
Code
hist_hawks = alt.Chart(samp).transform_bin(
'length',
field = 'length',
bin = alt.Bin(step = 2)
).transform_aggregate(
count = 'count()',
groupby = ['length']
).transform_calculate(
density = 'datum.count/1000',
length = 'datum.length + 1'
).mark_bar(size = 20).encode(
x = 'length:Q',
y = 'density:Q'
)
hist_hawks.configure_axis(
labelFontSize = 14,
titleFontSize = 16
)Recovering subpopulations
If we fit a mixture model with two components, amazingly, the mixture components accurately recover the distributions for each sex, even though this was a latent (unobserved) variable:
# configure and fit mixture model
gmm_hawks = mixture.GaussianMixture(n_components = 2)
gmm_hawks.fit(samp.length.values.reshape(-1, 1))
# compare components with subpopulations
print('gmm component means: ', gmm_hawks.means_.ravel())
print('population means by sex: ', np.sort(population_hawks.groupby('sex').mean().values.ravel()))
print('gmm component variances: ', gmm_hawks.covariances_.ravel())
print('population variances by sex: ', np.sort(population_hawks.groupby('sex').var().values.ravel()))gmm component means: [50.70543698 57.33071086]
population means by sex: [50.48194081 57.5749014 ]
gmm component variances: [ 8.60692088 10.12549367]
population variances by sex: [8.522606 9.39645762]Note that the means and variances are estimated from the sample but compared with the population values above.
GMM density estimate
Further, the density estimate fits reasonably well:
Code
# compute a grid of lengths
grid_hawks = np.linspace(population_hawks.length.min(), population_hawks.length.max(), num = 500)
dens = np.exp(gmm_hawks.score_samples(grid_hawks.reshape(-1, 1)))
gmm_smooth_hawks = alt.Chart(
pd.DataFrame({'length': grid_hawks, 'density': dens})
).mark_line(color = 'black').encode(
x = 'length',
y = 'density'
)
(hist_hawks + gmm_smooth_hawks).configure_axis(
labelFontSize = 14,
titleFontSize = 16
)Explore
Take 2 minutes with your neighbor and use the activity notebook to explore the following questions.
- What happens if you fit the GMM with different numbers of components?
- Does the solution change if the GMM is re-fitted?
Kernel smoothing
Kernel smoothing is a technique similar to KDE used to visualize and estimate relationships (rather than distributions).
We’ll use the GDP and life expectancy data from lab 3 to illustrate.
Code
# read in data and subset
life = pd.read_csv('data/life-gdp.csv')
life = life[life.Year == 2000].loc[:, ['Country Name', 'All', 'GDP per capita']]
life['GDP per capita'] = np.log(life['GDP per capita'])
life.rename(columns = {'GDP per capita': 'log_gdp', 'All': 'life_exp', 'Country Name': 'country'}, inplace=True)
# scatterplot
scatter = alt.Chart(
life
).mark_point().encode(
x = alt.X('log_gdp', scale = alt.Scale(zero = False), title = 'log(GDP/capita)'),
y = alt.Y('life_exp', scale = alt.Scale(zero = False), title = 'Life expectancy')
)
scatter.configure_axis(
labelFontSize = 14,
titleFontSize = 16
)The method
The technique consists in estimating trend by local weighted averaging; a kernel function is used to determine the exact weights.
ˆy(x)=∑iKb(xi−x)yi∑iKb(xi−x)
Example
Code
# calculate kernel smoother
kernreg = sm.nonparametric.KernelReg(endog = life.life_exp.values,
exog = life.log_gdp.values,
reg_type = 'lc',
var_type = 'c',
ckertype = 'gaussian')
# grid of gdp values
gdp_grid = np.linspace(life.log_gdp.min(), life.log_gdp.max(), num = 100)
# calculate kernel smooth at each value
fitted_values = kernreg.fit(gdp_grid)[0]
# arrange as data frame
pred_df = pd.DataFrame({'log_gdp': gdp_grid, 'life_exp': fitted_values})
# plot
kernel_smooth = alt.Chart(
pred_df
).mark_line(
color = 'black'
).encode(
x = 'log_gdp',
y = alt.Y('life_exp', scale = alt.Scale(zero = False))
)
(scatter + kernel_smooth).configure_axis(
labelFontSize = 14,
titleFontSize = 16
)Notice that the kernel smooth trails off a bit near the boundary – this is because fewer points are being averaged once the smoothing window begins to extend beyond the range of the data.
LOESS
Locally weighted scatterplot smoothing (LOESS or LOWESS) largely corrects this issue by stitching together lines (or low-order polynomials) fitted to local subsets of data; this way, near the boundary, the estimate still takes account of any trend present in the data.
LOESS example
Code
# fit loess smooth
loess = sm.nonparametric.lowess(endog = life.life_exp.values,
exog = life.log_gdp.values,
frac = 0.3,
xvals = gdp_grid)
# store as data frame
loess_df = pd.DataFrame({'log_gdp': gdp_grid, 'life_exp': loess})
# plot
loess_smooth = alt.Chart(
loess_df
).mark_line(
color = 'blue',
strokeDash = [8, 8]
).encode(
x = 'log_gdp',
y = alt.Y('life_exp', scale = alt.Scale(zero = False))
)
(scatter + loess_smooth).configure_axis(
labelFontSize = 14,
titleFontSize = 16
)Comparison
If we compare the LOESS curve with the kernel smoother, the different behavior on the boundary is evident:
Explore
Take 2-3 minutes with your neighbor and use the activity notebook to answer the following questions.
- Are there any bandwidths that give you a straight-line fit?
- What seems to be the minimum bandwidth?
- Which bandwidth best captures the pattern of scatter?