| GEOID_MSA | Name | Econ_Domain | Social_Domain | Env_Domain | Sustain_Index | |
|---|---|---|---|---|---|---|
| 0 | 310M300US10100 | Aberdeen, SD Micro Area | 0.565264 | 0.591259 | 0.444472 | 1.600995 |
| 1 | 310M300US10140 | Aberdeen, WA Micro Area | 0.427671 | 0.520744 | 0.429274 | 1.377689 |
Covariance and correlation
Invalid Date
This week
- Covariance and correlation
- Definitions
- Covariance and correlation matrices
- Eigendecomposition
- The eigenvalue problem
- Geometric interpretation
- Computations
- Principal components analysis
- PCA in the low-dimensional setting
- Variation capture and loss
- Interpreting principal components
- Dimension reduction
City sustainability data
We’ll use the dataset on the sustainability of U.S. cities introduced last time:
For each Metropolitan Statistical Area (MSA), a sustainability index is calculated based on economic, social, and environmental indicators (also indices):
sustainability index=economic+social+environmental
About the data
The domain indices are computed from a large number of development indicator variables.
If you’re interested, you can dig deeper on the Sustainable Development Report website, which provides detailed data reports related to the U.N.’s 2030 sustainable development goals.
What is covariation?
Covariation refers to the tendency of two variables to change together across observations. Covariation is about relationships.
Code
# scatterplot of social vs economic indices
econ_social = alt.Chart(city_sust).mark_point().encode(
x = alt.X('Econ_Domain', scale = alt.Scale(zero = False)),
y = alt.Y('Social_Domain', scale = alt.Scale(zero = False))
).properties(
width = 350,
height = 200
)
econ_social.configure_axis(
labelFontSize = 14,
titleFontSize = 16
)The social and economic indices do seem to vary together: higher values of the economic index coincide with higher values of the social index. That’s all there is to it.
How is covariation measured?
Let (x1,y1)…,(xn,yn) denote n values of two variables, X and Y.
If X and Y tend to vary together, then whenever X is far from its mean, so is Y: in other words, their deviations coincide.
This coincidence (or lack thereof) is measured quantiatively by the (sample) covariance:
cov(x,y)=1n−1n∑i=1(xi−ˉx)(yi−ˉy)
Note cov(x,x)=var(x).
As an inner product
The sum can be written as an inner product. First, ‘center’ x and y:
˜x=[x1−ˉx⋮xn−ˉx]˜y=[y1−ˉy⋮yn−ˉy]
Then, the sample covariance is:
cov(x,y)=˜xT˜yn−1
Correlation: standardized covariance
Covariance is a little tricky to interpret. Is 0.00199 large or small?
It is more useful to compute the (sample) correlation:
corr(x,y)=cov(x,y)SxSy
This is simply a standardized covariance measure.
corr(x,y)=1,−1 are the strongest possible correlations
corr(x,y)=0 is the weakest possible correlation
the sign indicates whether X and Y vary together or in opposition
corr(x,x)=1, since any variable’s deviations coincide perfectly with themselves
Correlation of social and economic indices
Standardizing the covariance makes it more interpretable:
The correlation indicates that the social and economic indices vary together (positive) moderately (halfway from zero to one).
This is just a number that quantifies what you already knew from the graphic: there is a positive relationship.
Aside: other correlations
What we will call ‘correlation’ in this class is known as the Pearson correlation coefficient.
There are other correlation measures:
- Spearman correlation: Pearson correlation between ranks of observations
- Kendall rank correlation
- Distribution-specific dependence measures (e.g., circular data)
Common micsonceptions
No correlation does not imply no relationship – symmetry can produce strongly related but uncorrelated data.
Code
np.random.seed(50323)
# simulate observations of x
n = 100
x = np.random.uniform(low = 0, high = 1, size = n)
sim_df = pd.DataFrame({'x': x})
# center x, center y, scale
a, b, c = 0.5, 0.5, 3
# noise
noise_sd = 0.1
noise = np.random.normal(loc = 0, scale = noise_sd, size = n)
# simulate observations of y
sim_df['y'] = c*(x - a)*(x - b) + noise
# plot
scatter = alt.Chart(
sim_df
).mark_point().encode(
x = 'x',
y = 'y'
)
# compute correlation
print('correlation: ', sim_df.corr().loc['x', 'y'])
scatter.configure_axis(
labelFontSize = 14,
titleFontSize = 16
)correlation: 0.07227477481863404Code
np.random.seed(50323)
# simulate observations of x
n = 100
x = np.random.uniform(low = 0, high = 1, size = n)
sim_df = pd.DataFrame({'x': x})
# center x, center y, scale
a, b, c = 0.5, 0.5, 3
# noise
noise_sd = 0.2
noise = np.random.normal(loc = 0, scale = noise_sd, size = n)
# simulate observations of y
sim_df['y'] = np.cos(4*np.pi*x) + noise
# plot
scatter = alt.Chart(
sim_df
).mark_point().encode(
x = 'x',
y = 'y'
)
# compute correlation
print('correlation: ', sim_df.corr().loc['x', 'y'])
scatter.configure_axis(
labelFontSize = 14,
titleFontSize = 16
)correlation: 0.04482962033696271Linearity
Correlation measures the strength of linear relationships. But what does “strength” mean exactly?
- cor(x,y)=1 implies the data lie exactly on a line with positive slope
- cor(x,y)=−1 implies the data lie exactly on a line with negative slope
- cor(x,y)=0 implies that the best linear fit to the data is a horizontal line
- values near 1 or −1 imply the data lie near a line with nonzero slope
More common misconceptions
Correlations are affected by outliers – low correlation does not imply no relationship.
Code
np.random.seed(50423)
# intercept, slope
a, b = 1, -1
# noise
noise_sd = 0.1
noise = np.random.normal(loc = 0, scale = noise_sd, size = n)
# simulate y
sim_df['y'] = a + b*x + noise
sim_df.loc[100] = [3, 3]
# plot
scatter = alt.Chart(
sim_df
).mark_point().encode(
x = 'x',
y = 'y'
)
# compute correlation
print('correlation: ', sim_df.corr().loc['x', 'y'])
sim_df = sim_df.loc[0:99].copy()
scatter.configure_axis(
labelFontSize = 14,
titleFontSize = 16
)correlation: -0.057700019900550986More common misconceptions
A strong correlation does not imply a meaningful relationship – it could be practically insignificant.
Code
np.random.seed(50423)
# intercept, slope
a, b = -0.002, 0.005
# noise
noise_sd = 0.001
noise = np.random.normal(loc = 0, scale = noise_sd, size = 100)
# simulate y
sim_df['y'] = a + b*x + noise
# plot
scatter = alt.Chart(
sim_df
).mark_point().encode(
x = alt.X('x', title = 'rate'),
y = alt.Y('y', title = 'earnings (USD)')
)
# compute correlation
print('correlation: ', sim_df.corr().loc['x', 'y'])
scatter.configure_axis(
labelFontSize = 14,
titleFontSize = 16
)correlation: 0.794145106831753More common misconceptions
A weak correlation does not imply no linear relationship – it could just be really noisy.
Code
np.random.seed(50423)
# intercept, slope
a, b = 1, -3
# noise
noise_sd = 4
noise = np.random.normal(loc = 0, scale = noise_sd, size = 100)
# simulate y
sim_df['y'] = a + b*x + noise
# plot
scatter = alt.Chart(
sim_df
).mark_point().encode(
x = 'x',
y = 'y'
)
trend = scatter.transform_regression('x', 'y').mark_line()
# compute correlation
print('correlation: ', sim_df.corr().loc['x', 'y'])
(scatter + trend).configure_axis(
labelFontSize = 14,
titleFontSize = 16
)correlation: -0.2552753897590402Why measure at all?
It helps to have a number to quantify the strength of a relationship.
For instance, which pair is most related? Are some pairs more related than others?
Code
# extract social and economic indices
x_mx = city_sust.iloc[:, 2:5]
# long form dataframe for plotting panel
scatter_df = x_mx.melt(
var_name = 'row',
value_name = 'row_index'
).join(
pd.concat([x_mx, x_mx, x_mx], axis = 0).reset_index(),
).drop(
columns = 'index'
).melt(
id_vars = ['row', 'row_index'],
var_name = 'col',
value_name = 'col_index'
)
# panel
alt.Chart(scatter_df).mark_point(opacity = 0.4).encode(
x = alt.X('row_index', scale = alt.Scale(zero = False), title = ''),
y = alt.Y('col_index', scale = alt.Scale(zero = False), title = '')
).properties(
width = 150,
height = 75
).facet(
column = alt.Column('col', title = ''),
row = alt.Row('row', title = '')
).resolve_scale(x = 'independent', y = 'independent')Correlations give us an exact and concise answer, despite their imperfection.
Correlation matrix
The pairwise correlations among all three variables can be represented in a simple square matrix:
# extract social and economic indices
x_mx = city_sust.iloc[:, 2:5]
# compute matrix of correlations
x_mx.corr()| Econ_Domain | Social_Domain | Env_Domain | |
|---|---|---|---|
| Econ_Domain | 1.000000 | 0.531491 | 0.011206 |
| Social_Domain | 0.531491 | 1.000000 | -0.138674 |
| Env_Domain | 0.011206 | -0.138674 | 1.000000 |
The strongest linear relationship is between social and economic indices; the weakest is between environmental and economic indices.
Covariance matrix
Let X denote n observations of p variables: X=[x1x2⋯xp]
The (sample) covariance matrix is: cov(X)=[cov(x1,x1)cov(x1,x2)⋯cov(x1,xp)cov(x2,x1)cov(x2,x2)⋯cov(x2,xp)⋮⋮⋱⋮cov(xp,x1)cov(xp,x2)⋯cov(xp,xp)]
It is easy to calculate as a matrix product after centering the data:
cov(X)=(X−ˉX)T(X−ˉX)n−1
Here ˉX is a matrix whose rows are n copies of the column means of X.
Correlation matrix
The (sample) correlation matrix is, similarly, the matrix of pariwise correlations:
corr(X)=[corr(x1,x1)corr(x1,x2)⋯corr(x1,xp)corr(x2,x1)corr(x2,x2)⋯corr(x2,xp)⋮⋮⋱⋮corr(xp,x1)corr(xp,x2)⋯corr(xp,xp)]
And can be obtained by standardizing the covariance matrix:
corr(X)=(diag(cov(X)))−1/2[cov(X)](diag(cov(X)))−1/2
Correlation matrix
For another perspective, the correlation matrix can be seen as the covariance after normalizing. Consider: Z={xij−ˉxjsxj}=[x11−ˉx1sx1⋯x1p−ˉxpsxpx21−ˉx1sx1⋯x2p−ˉxpsxp⋮⋱⋮xn1−ˉx1sx1⋯xnp−ˉxpsxp]
The (sample) correlation matrix is then:
corr(X)=cov(Z)=Z′Zn−1⏟call this R
Calculations
# correlation matrix 'by hand'
n = len(x_mx) # sample size
z_mx = (x_mx - x_mx.mean())/x_mx.std() # (xi - xbar)/sx
z_mx.transpose().dot(z_mx)/(n - 1) # Z'Z/(n - 1)| Econ_Domain | Social_Domain | Env_Domain | |
|---|---|---|---|
| Econ_Domain | 1.000000 | 0.531491 | 0.011206 |
| Social_Domain | 0.531491 | 1.000000 | -0.138674 |
| Env_Domain | 0.011206 | -0.138674 | 1.000000 |
Luckily, df.cov() and df.cor() will do all the work for you:
However, you should understand and be able to verify the calculations.
Heatmap visualization
Code
# store correlation matrix
corr_mx = x_mx.corr()
# melt to long form
corr_mx_long = corr_mx.reset_index().rename(
columns = {'index': 'row'}
).melt(
id_vars = 'row',
var_name = 'col',
value_name = 'Correlation'
)
# visualize
alt.Chart(corr_mx_long).mark_rect().encode(
x = alt.X('col', title = '', sort = {'field': 'Correlation', 'order': 'ascending'}),
y = alt.Y('row', title = '', sort = {'field': 'Correlation', 'order': 'ascending'}),
color = alt.Color('Correlation',
scale = alt.Scale(scheme = 'blueorange',
domain = (-1, 1),
type = 'sqrt'),
legend = alt.Legend(tickCount = 5))
).properties(width = 200, height = 200)Each cell corresponds to a pair of variables
Cells are colored acccording to the magnitude of correlation between the pair
Rows and columns are sorted in order of correlation strength
Diverging color scale should always be used!
Higher dimensions
Consider a larger collection of development-related variables measured on countries:
Code
wdi = pd.read_csv('data/wdi-data.csv').iloc[:, 2:].set_index('country')
# store correlation matrix
corr_mx = wdi.corr()
# melt to long form
corr_mx_long = corr_mx.reset_index().rename(
columns = {'index': 'row'}
).melt(
id_vars = 'row',
var_name = 'col',
value_name = 'Correlation'
)
# visualize
alt.Chart(corr_mx_long).mark_rect().encode(
x = alt.X('col', title = '', sort = {'field': 'Correlation', 'order': 'ascending'}),
y = alt.Y('row', title = '', sort = {'field': 'Correlation', 'order': 'ascending'}),
color = alt.Color('Correlation',
scale = alt.Scale(scheme = 'blueorange',
domain = (-1, 1),
type = 'sqrt'),
legend = alt.Legend(tickCount = 5))
).configure_axis(
labelFontSize = 14
).configure_legend(
labelFontSize = 14,
titleFontSize = 16
)Higher dimensions
For larger collections of variables, we might wish to:
- find a simplified representation of the correlation structure
- visualize the data in a lower-dimensional space
Factoring the correlation matrix provides a means of doing both. We’ll use eigendecomposition.
The eigenvalue problem
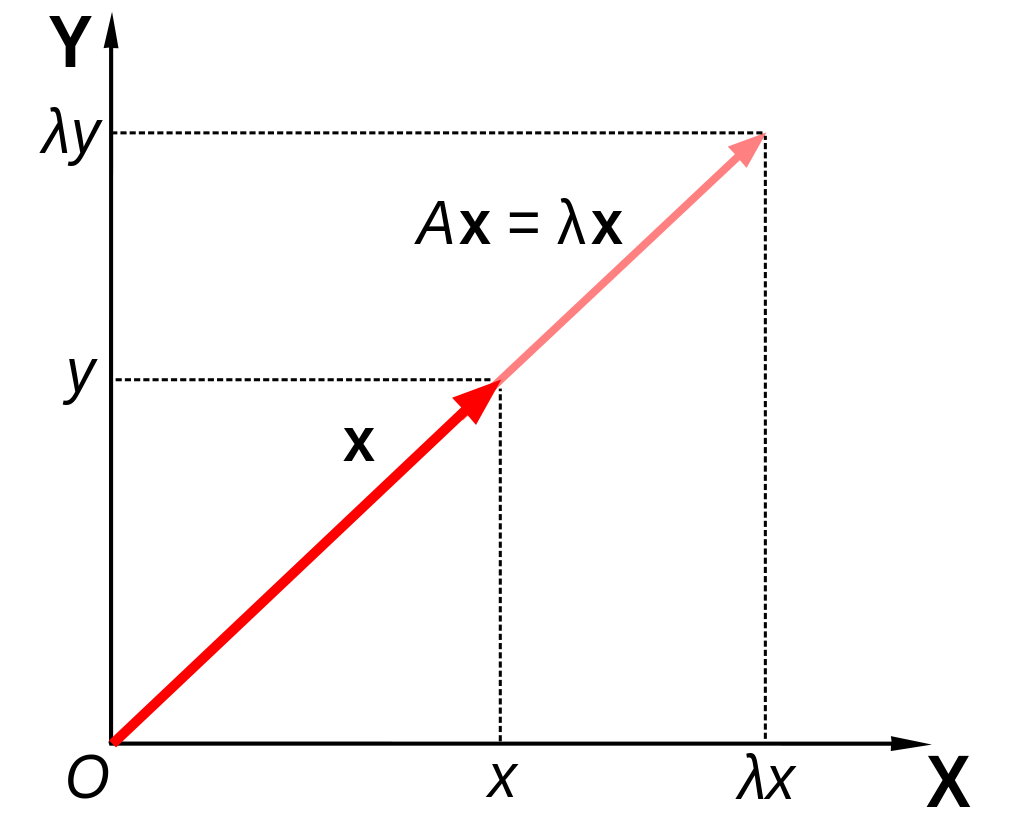
Let A be a square (n×n) matrix.
The eigenvalue problem refers to finding nonzero λ and x that satisfy the equation:
Ax=λx
For any such solutions:
- λ is an eigenvalue of A;
- x is an eigenvector of A.
Geometry
For a simple example, suppose n=2 and x is an eigenvalue of A. Then:
Ax=[a11a12a21a22][x1x2]=[a11x1+a12x2a21x1+a22x2]=[λx1λx2]=λx
So the eigenvalue problem equation says that the linear transformation of x by A is simply a rescaling of x by a factor of λ.
Eigendecomposition
The eigendecomposition of a square matrix consists in finding the eigenvalues and eigenvectors.
This is considered a ‘decomposition’ because the eigenvectors V and eigenvalues Λ satisfy
A⏟original matrix=VΛV′⏟eigendecomposition
It’s also known as the ‘spectral decomposition’.
So the original matrix can be reconstructed from the eigenvalues and eigenvectors.
Uniqueness
If λ,x are solutions, then so are cλ,cx for any constant c.
So assume that ‖x‖=1.
Then solutions are unique to within the sign of x.
Special case
We will be applying eigendecomposition to correlation matrices, which have a special form A=Z′Z.
One can show that for matrices of this form:
- V′V=I, in other words, the eigenvectors are an orthonormal basis
- columns of V are orthogonal
- columns of V are of unit length
- λi≥0, in other words, all eigenvalues are nonnegative
Computations
The eigendecomposition is computed numerically using iterative methods. Luckily, these are very easy to implement:
Does the decomposition really work?
Let’s check that in fact A=VΛV′:
Orthogonality
Let’s check also that in fact V′V=I:
The significance of this property is that v1,v2,v3 form an orthonormal basis.
What’s a basis?
A basis in linear algebra is a set of vectors that span a linear space. Think of a basis as a set of axes.
For instance, the usual basis for R3 are the unit vectors: e1=(1,0,0)e2=(0,1,0)e3=(0,0,1)
The usual coordinates in R3 in fact refer to multiples of these basis vectors: (1,2,1)=1e1+2e2+1e3
A basis is orthogonal if all basis vectors are at right angles to one another
A basis is orthonormal if it is orthogonal and basis vectors are of unit length
Nonstandard bases
To an extent the usual choice of e1,e2,e3 is arbitrary.
It’s possible to choose any system based on three directions to represent the same point relative to the origin.
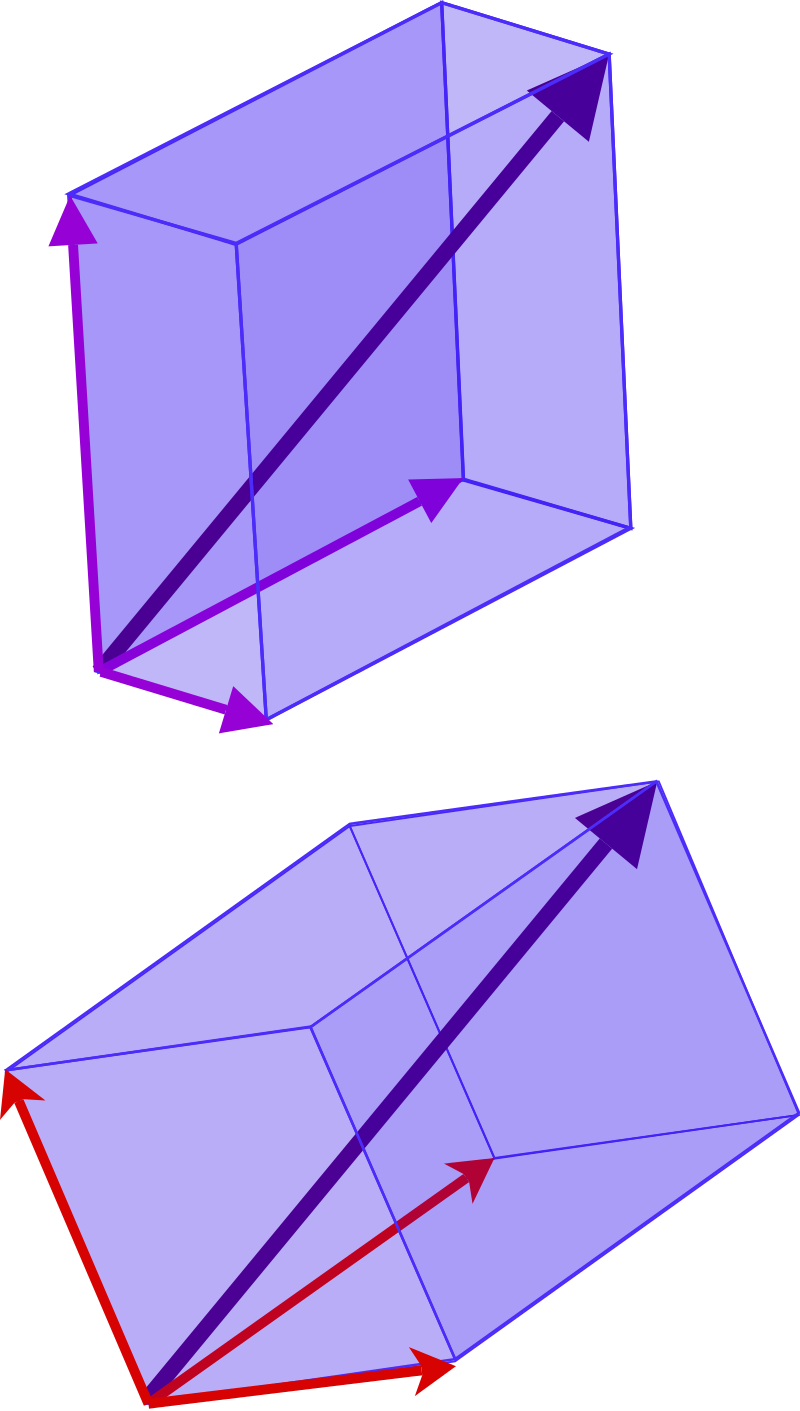
Change of basis
Different bases are simply different coordinate systems.
It’s akin to the possibility of locating the distance to the corner store by different units and relative to different directions. For example:
half a block to the right from the front door; or
sixty steps diagonally in a straight line; or
fifteen steps north, fifty steps east.
Basis from correlations
Decomposing the correlation matrix yields a basis for Rp – when standardized data are represented on that basis, observations become uncorrelated.
Let Y=ZV; this is the representation of Z on the basis given by V.
Then: Y′Y=V′Z′ZV=V′VΛV′V=Λ
Together with the observation that ˉY=0, this implies that cov(yj,yk)=0 since Λ is diagonal.
Decorrelating data
We can easily verify this property by computing cor(ZV):
The columns are now orthogonal:
Capturing variation
The eigenbasis from the correlation matrix in a sense ‘captures’ the covariation in the data.
- provides a coordinate system on which the (standardized) data are uncorrelated
- coordinate axes are the ‘main’ directions of total variability (will demonstrate empirically)
Those ‘main directions’ are known as principal components.
Other decompositions
The eigenbasis from the correlation matrix can also be recovered from the singular value decomposition of Z.
Z=UDV′⟹Z′Z=V(D′U′UD)⏟ΛV′
In fact, most implementations of principal components use the SVD instead of eigendecomposition.