array([0.01929165])Prediction
Invalid Date
From last week
Simple linear regression model: \[ y_i = \beta_0 + \beta_1 x_i + \epsilon_i \quad \begin{cases} i = 1, \dots, n \\ \epsilon_i \sim N\left(0,\sigma^2\right) \end{cases} \]
- estimation of \(\beta_0, \beta_1, \sigma^2\)
- standard errors for the coefficients
- parameter interpretations
Example using the SEDA data:
\[ \left(\text{math gap}\right)_i = \beta_0 + \beta_1 \log\left(\text{median income}\right)_i + \epsilon_i \quad \text{district } i = 1, \dots, 625 \]
- \(\hat{\beta_0} = -1.356, \hat{\beta_1} = 0.121, \hat{\sigma}^2 = 0.0132\)
- centering the explanatory variable helped with interpretability
Where we left off
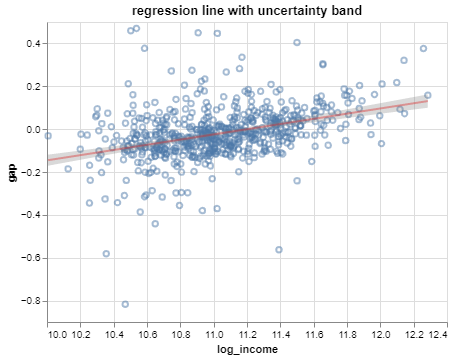
Uncertainty bands are a common visualization technique for conveying variability in estimates.
- constructed using standard errors
- but how?
Predictions
The line we are visualizing shows model predictions across the range of the data:
\[ \hat{y} = \hat{\beta}_0 + \hat{\beta}_1 x \;,\quad x \in [x_\text{min}, x_\text{max}] \]
- same calculation as for the fitted values
- but predictions because we didn’t fit the model to \(x \in [x_\text{min}, x_\text{max}]\)
Predictions
If for example, we’d like to make a prediction for a district with a median income of 86K, we’d calculate: \[ \hat{\beta}_0 + \hat{\beta}_1\log(86000) \]
In statsmodels, there is a .predict method to perform this basic calculation:
Note that this returns a numpy array. The uncertainty bands are intervals constructed around such predictions for a fine grid of values on the interval \([x_\text{min}, x_\text{max}]\).
Two types of prediction
The prediction \(\hat{y}\) is an estimate, but what of?
Two options:
- estimate of the mean at \(x\): \[ \mathbb{E}y = \beta_0 + \beta_1 x \]
- estimate of an observation at \(x\) \[ y = \beta_0 + \beta_1 x + \epsilon \]
Standard error for the mean
If we interpret \(\hat{y}\) as a prediction for the mean, the standard error is based on: \[ \text{var}\left(\hat{\beta}_0 + \hat{\beta}_1 x\right) = \text{var}\hat{\beta}_0 + x^2 \text{var}\hat{\beta}_1 + 2x\text{cov}\left(\hat{\beta}_0, \hat{\beta}_1\right) \]
To get the standard error (estimated standard deviation), substitute \(\hat{\sigma}^2\) for \(\sigma^2\) and take the square root.
Standard error for the observation
If instead we interpret \(\hat{y}\) as a prediction for a new observation, the standard error is based on:
\[ \text{var}\left(\hat{\beta}_0 + \hat{\beta}_1 x + \epsilon\right) = \text{var}\hat{\beta}_0 + x^2 \text{var}\hat{\beta}_1 + 2x\text{cov}\left(\hat{\beta}_0, \hat{\beta}_1\right) + \text{var}\epsilon \]
The above holds because we assume the future random error is independent of current observations (and thus the estimates).
To get the standard error (estimated standard deviation), substitute \(\hat{\sigma}^2\) for \(\sigma^2\) and take the square root.
Computing standard errors
The .get_prediction() returns a prediction object with several attributes, including standard errors. This is recommended over .predict() for most purposes.
<statsmodels.regression._prediction.PredictionResults at 0x1218c9690>Standard errors, in matrix form
The variance of the estimated mean at \(\mathbf{x}_{new}\) is: \[ \text{var}(\widehat{\mathbb{E}y_\text{new}}) = \mathbf{x}_\text{new} \; \underbrace{ \left[\sigma^2 (\mathbf{X'X})^{-1}\right] }_{ \text{var}\hat{\beta} }\; \mathbf{x}_\text{new}' \]
So the standard error is obtained by substituting \(\hat{\sigma}\) for \(\sigma\): \[ SE\left(\widehat{\mathbb{E}y_\text{new}}\right) = \sqrt{\hat{\sigma}^2\left(\mathbf{x}_\text{new}'(\mathbf{X'X})^{-1}\mathbf{x}_\text{new}\right)} \]
Standard errors, in matrix form
The variance of a predicted observation at \(\mathbf{x}_{new}\) is: \[ \text{var}(y_\text{new}) = \underbrace{ \mathbf{x}_\text{new} \left[\hat{\sigma}^2 (\mathbf{X'X})^{-1}\right] \mathbf{x}_\text{new}' }_{SE^2\left(\widehat{\mathbb{E}y_\text{new}}\right)} + \hat{\sigma}^2 \]
So the standard error is obtained by substituting \(\hat{\sigma}\) for \(\sigma\): \[ SE\left(y_\text{new}\right) = \sqrt{\hat{\sigma}^2\left(1 + \mathbf{x}_\text{new}'(\mathbf{X'X})^{-1}\mathbf{x}_\text{new}\right)} \]
Comparing standard errors
Note the substantial difference between the standard error for the mean and that for the observation:
print('standard error for mean: ', pred.se_mean)
print('standard error for observation: ', pred.se_obs)standard error for mean: [0.00605441]
standard error for observation: [0.11492531]Why is one so much larger??
Sources of variability
There is only one source of variability for a predicted mean:
- variability of the estimates \(\hat{\beta}_j\)
There are two sources of variability for a predicted observation:
- variability of the estimates \(\hat{\beta}_j\)
- variability of the random error \(\epsilon\)
Interpreting standard errors
The standard error for the mean is smaller, because it’s easier to estimate the average value for a given \(x\) than the exact value:
- (less uncertainty) the typical achievement gap for a district with a given median income
- (more uncertainty) the precise achievement gap for such-and-such district
The two standard errors will differ substantially whenever there is a lot of unexplained variability (\(low R^2\)).
Uncertainty bands
The uncertainty bands from before were \(\hat{y} \pm 2SE(\hat{y})\)
Technically, a confidence interval; usually shown for the mean (not the observation).
Code
# compute predictions at observed values
preds = slr.fit().get_prediction(x)
# append fitted values to observations
regdata['fitted'] = preds.predicted_mean
# add interval bounds
regdata['lwr_mean'] = preds.predicted_mean - 2*preds.se_mean
regdata['upr_mean'] = preds.predicted_mean + 2*preds.se_mean
scatter = alt.Chart(regdata).mark_circle().encode(
x = alt.X('log_income',
scale = alt.Scale(zero = False),
title = 'log median income'),
y = alt.Y('gap', title = 'math achievement gap')
)
trend = alt.Chart(regdata).mark_line(
color = 'black'
).encode(
x = 'log_income',
y = 'fitted'
)
band = alt.Chart(regdata).mark_area(
opacity = 0.3, color = 'black'
).encode(
x = 'log_income',
y = 'upr_mean',
y2 = 'lwr_mean'
)
(scatter + trend + band).configure_axis(
labelFontSize = 16,
titleFontSize = 18
)Prediction bands
The same figure constructed using the standard error for observations is:
Code
# add interval bounds
regdata['lwr_obs'] = preds.predicted_mean - 2*preds.se_obs
regdata['upr_obs'] = preds.predicted_mean + 2*preds.se_obs
scatter = alt.Chart(regdata).mark_circle().encode(
x = alt.X('log_income',
scale = alt.Scale(zero = False),
title = 'log median income'),
y = alt.Y('gap', title = 'math achievement gap')
)
trend = alt.Chart(regdata).mark_line(
color = 'black'
).encode(
x = 'log_income',
y = 'fitted'
)
band = alt.Chart(regdata).mark_area(
opacity = 0.3, color = 'black'
).encode(
x = 'log_income',
y = 'upr_obs',
y2 = 'lwr_obs'
)
(scatter + trend + band).configure_axis(
labelFontSize = 16,
titleFontSize = 18
)Confidence interval for the mean
Prediction objects come equipped with a method .conf_int() for computing confidence intervals.
By default, these will return 95% intervals for the mean. For the prediction at median income of 86K:
Interpretation:
With 95% confidence, the mean achievement gap for a district with median income of 86K is estimated to favor boys by between 0.0074 and 0.0312 standard deviations from the national average.
Prediction intervals
The same method can return prediction intervals for observations. Set obs = True to use the standard error for observations:
Interpretation:
With 95% confidence, the precise achievement gap for a district with median income of 86K is estimated to be between 0.206 standard deviations favoring girls and 0.245 standard deviations favoring boys.
Confidence level
The multiplier 2 gives an approximate 95% interval.
We can change that multiplier to obtain an interval for a different confidence level.
The confidence level is simply the percentage of the time that the interval covers the true value.
- the 95% interval contains the observation of interest for 95% of samples
- the 90% interval contains the observation of interest for 90% of samples
.summary_frame()
The .summary_frame() method is handy for dealing with multiple predictions:
# explanatory variable array for 4 new observations
income_new = np.linspace(10000, 100000, 4)
x_new = sm.tools.add_constant(np.log(income_new))
# compute predictions
pred = slr.fit().get_prediction(x_new)
# generate point estimates and intervals
pred_df = pred.summary_frame(alpha = 0.1)
pred_df['log_income'] = np.log(income_new)
pred_df| mean | mean_se | mean_ci_lower | mean_ci_upper | obs_ci_lower | obs_ci_upper | log_income | |
|---|---|---|---|---|---|---|---|
| 0 | -0.241194 | 0.022020 | -0.277468 | -0.204920 | -0.433697 | -0.048692 | 9.210340 |
| 1 | -0.073374 | 0.006875 | -0.084699 | -0.062048 | -0.262766 | 0.116019 | 10.596635 |
| 2 | -0.005628 | 0.004832 | -0.013589 | 0.002332 | -0.194850 | 0.183593 | 11.156251 |
| 3 | 0.037550 | 0.007345 | 0.025450 | 0.049649 | -0.151891 | 0.226991 | 11.512925 |
A summary dataframe computed on a prediction grid returns the raw materials needed to plot uncertainty bands of different levels/types.
Check your understanding
Which is the prediction band and which is the mean? Why?
Code
# construct prediction grid
income_grid = np.logspace(start = 10, stop = 12.5, num = 200, base = np.e)
x_grid = sm.tools.add_constant(np.log(income_grid))
# compute predictions
preds = slr.fit().get_prediction(x_grid)
pred_df = preds.summary_frame(alpha = 0.05)
pred_df['log_income'] = np.log(income_grid)
# visualization
trend = alt.Chart(pred_df).mark_line(
color = 'black'
).encode(
x = 'log_income',
y = 'mean'
)
band = alt.Chart(pred_df).mark_area(
opacity = 0.3, color = 'black'
).encode(
x = 'log_income',
y = 'mean_ci_lower',
y2 = 'mean_ci_upper'
)
(scatter + trend + band).configure_axis(
labelFontSize = 14,
titleFontSize = 16
)Code
# construct prediction grid
income_grid = np.logspace(start = 10, stop = 12.5, num = 200, base = np.e)
x_grid = sm.tools.add_constant(np.log(income_grid))
# compute predictions
preds = slr.fit().get_prediction(x_grid)
pred_df = preds.summary_frame(alpha = 0.05)
pred_df['log_income'] = np.log(income_grid)
# visualization
trend = alt.Chart(pred_df).mark_line(
color = 'black'
).encode(
x = 'log_income',
y = 'mean'
)
band = alt.Chart(pred_df).mark_area(
opacity = 0.3, color = 'black'
).encode(
x = 'log_income',
y = 'obs_ci_lower',
y2 = 'obs_ci_upper'
)
(scatter + trend + band).configure_axis(
labelFontSize = 14,
titleFontSize = 16
)Check your understanding
Which is the 99% band and which is the 85% band? Why?
Code
# construct prediction grid
income_grid = np.logspace(start = 10, stop = 12.5, num = 200, base = np.e)
x_grid = sm.tools.add_constant(np.log(income_grid))
# compute predictions
preds = slr.fit().get_prediction(x_grid)
pred_df = preds.summary_frame(alpha = 0.01)
pred_df['log_income'] = np.log(income_grid)
# visualization
trend = alt.Chart(pred_df).mark_line(
color = 'black'
).encode(
x = 'log_income',
y = 'mean'
)
band = alt.Chart(pred_df).mark_area(
opacity = 0.3, color = 'black'
).encode(
x = 'log_income',
y = 'mean_ci_lower',
y2 = 'mean_ci_upper'
)
(scatter + trend + band).configure_axis(
labelFontSize = 14,
titleFontSize = 16
)Code
# construct prediction grid
income_grid = np.logspace(start = 10, stop = 12.5, num = 200, base = np.e)
x_grid = sm.tools.add_constant(np.log(income_grid))
# compute predictions
preds = slr.fit().get_prediction(x_grid)
pred_df = preds.summary_frame(alpha = 0.15)
pred_df['log_income'] = np.log(income_grid)
# visualization
trend = alt.Chart(pred_df).mark_line(
color = 'black'
).encode(
x = 'log_income',
y = 'mean'
)
band = alt.Chart(pred_df).mark_area(
opacity = 0.3, color = 'black'
).encode(
x = 'log_income',
y = 'mean_ci_lower',
y2 = 'mean_ci_upper'
)
(scatter + trend + band).configure_axis(
labelFontSize = 14,
titleFontSize = 16
)Predictive accuracy
How good are the predictions?
The standard measure of accuracy is mean square error (MSE):
\[ MSE(y, \hat{y}) = \frac{1}{n}\sum_i (y_i - \hat{y}_i)^2 \]
Similar to a variance, but measures the spread of observations about the predictions rather than their spread about the sample mean.
Expected squared error
MSE is an estimate of \(\mathbb{E}(y - \hat{y})^2\).
For genuine predictions, \(y_i\) and \(\hat{y}_i\) are uncorrelated, because:
- new observations are independent of past observations
- the prediction depends only on past observations (through \(\hat{\beta}\))
As a result one can show: \[ \mathbb{E}(y_i - \hat{y}_i)^2 = \text{var}\epsilon_i + \text{var}\hat{y}_i \]
- The expected squared error is the variance of the observation plus the variance of the prediction.
- Larger expected prediction errors come from high prediction variance or high observation variance or both.
Data partitioning
If fitted values are used to calculate MSE, \(y_i\) and \(\hat{y}_i\) will be correlated, and MSE will be biased.
Another way of understanding: the model will have an advantage on the data that it was fit to.
To avoid this problem, it is common practice to partition data into nonoverlapping subsets:
- one used to fit the model
- another used to evaluate predictions